徐鹏教授课题组聚焦于“集成电路及器件电磁分析”，主要涉及目标（含人工目标）的电磁计算及分析。现有教授1名，副教授2名，讲师5名。在“薄膜体声波滤波器性能分析”，“基于深度学习的超表面相位响应的预测”，“基于机器学习的射频芯片设计”，“深度学习的微波滤波器设计”研究方面获得了多项企业和湖北省教育厅项目资助。从2019年开始利用深度学习方法预测像素化超表面的幅度和相位响应，进而制备微波器件，建立了一套基于深度学习的超表面微波器件的设计平台，解决了超表面设计和优化的周期时间长的难题，大大缩短了超表面微波器件设计的时间和成本。已公开在Optics Communication, IEEE Geoscience and Remote Sensing Letters, Physics Letters A, Materials，Progress In Electromagnetics Research Letters等期刊发表50余篇论文，拥有发明专利3项，软件著作1项。
徐鹏，教授，IEEE会员，湖北工业大学芯片产业学院微电子系主任，集成电路及器件电磁分析科研团队负责人。IEEE TGRS、IEEE GRSL、IEEE JSTARS、Radio Science、PIER等国际期刊审稿人，国家基金委信息学部、地学部青年及面上项目通讯评审人，教育部学位中心通讯评议人。曾主持国家基金委面上项目2项，参与重点项目1项。在IEEE系列、Radio Science、PIER、MOTL、武大学报等期刊发表论文30余篇，在IEEE系列、URSI GASS、PIERS等发表会议论文20余篇。
徐鹏课题组部分研究成果分为：
1.电磁快速算法研究
2.微波遥感机理研究
3.超材料电磁特性研究
4.用于通信的电波传输研究
5.其它
一、电磁快速算法
工欲善其事，必先利其器。电磁数值计算的瓶颈之一就是对内存的需求O（N2）、对CPU时间需求O（N3）量级，实际目标数值离散后的未知量N少则几万，多则上千万，没有快速算法是很难在计算机上实现的。利用电磁快速算法，可将内存和CPU时间均将为O（NlogN）量级。然而针对不同的物理问题，没有一种快速算法是包打天下的，都有各自的缺陷，本人提出UV-FMM和UV-SMCG两个混合快速算法，克服了单独算法的缺陷，同时将各自优势发挥出来，前者能求解厚长目标的电磁散射，后者能求解更大电长度目标的电磁散射。
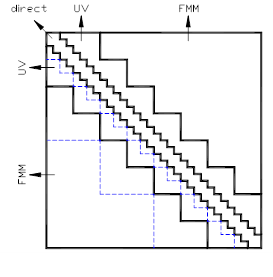
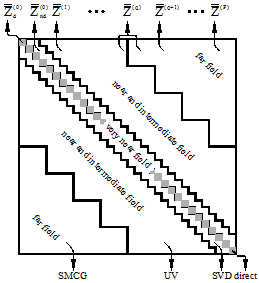
（a）UV-FMM混合快速算法 （b）UV-SMCG混合快速算法
图1 混合快速算法多层结构
P. Xu and L. Tsang, “Propagation over terrain and urban environment using the multilevel UV method and a hybrid UV/SDFMM method,” IEEE Antennas & Wireless Propag. Lett., vol.3, pp. 336-339, 2004.
P. Xu and L. Tsang, “Scattering by rough surface using a hybrid technique combining the multilevel UV method with the sparse matrix canonical grid method,” Radio Science, vol. 40, no. 4, RS4012, 2005.
二、微波遥感机理
Windsat测量数据首先发现格陵兰岛雪原水平和垂直极化亮温显著下降、第三和第四个Stokes参数比正常数值约大8倍。本人从电磁仿真研究上，均得到水平、垂直极化亮温显著降低，第三、第四Stokes参数异常的数值结果，并发现内部全反射和表面梯度大是导致其异常的主要原因，较好地解释了Windsat观测结果。
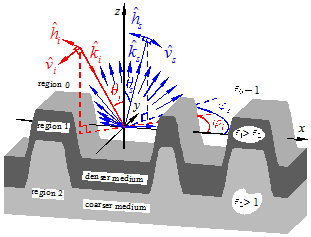
图2 双层波状随机粗糙面模型结构
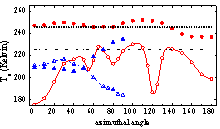
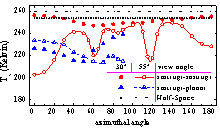
(a) 水平极化亮温 (b) 垂直极化亮温
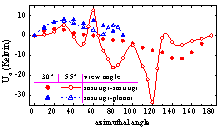
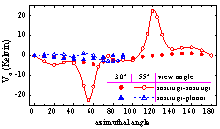
(c) 第三Stokes参数 (d) 第四Stokes参数
图3 C波段下四个Stokes参数随方位角变化的数值结果。本模型结果如红色圆圈记号所示。观察角较大（55°）时，Stokes参数更异常（带圈实线）。若第二交界面为平面，结果如蓝色三角形记号所示，第四Stokes参数较小
P. Xu, K. S. Chen, et al., “Full-wave simulation and analysis of bistatic scattering and polarimetric emissions from double-layered sastrugi surfaces,” IEEE Trans. Geosci. Remote Sens., vol. 55, no. 1, pp. 292-307, 2017.
三、超材料电磁特性
左手介质随机粗糙面电磁散射、透射和吸收的反常物理现象研究，是偶然发现的。如图4a所示，正常的右手介质（RHM）随着粗糙度增加，因变相地增加了吸波表面积，所以其对TE和TM极化电磁波吸收率均不断变大，直至饱和。然而，左手介质对TE波的吸收却随粗糙度的增加不断减小，并且对TM波的吸收是先增后减。左手介质的反常吸收，作者利用负折射所造成的二次反向透射进行了完美物理解释，也利用布儒斯特角的影响完美解释了左手介质本身TE和TM波的吸收为何不同。图4b更清晰地表明：粗糙度对右手介质吸收率贡献（即粗糙面吸收率减去平面吸收率）是正效应，对左手介质的TE波吸收却完全是负效应，TM波吸收则是先正后负效应。另外，从图5所示可看出，左手介质的反常吸收效应是不同入射角下的普遍现象。
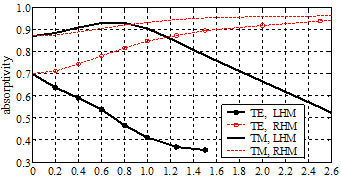
（a）电磁波吸收率随粗糙度（均方根高度）的变化曲线
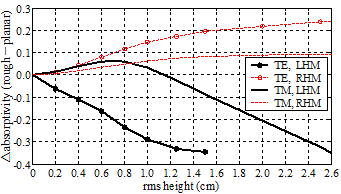
（b）粗糙度对吸收率贡献随粗糙度（均方根高度）的变化曲线
图4 左手介质和右手介质指数相关随机粗糙面的电磁吸收率对比。频率f=10.5 GHz，相关长度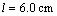
，
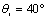，右手、左手介质的介电常数、磁导率分别为
，
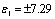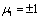
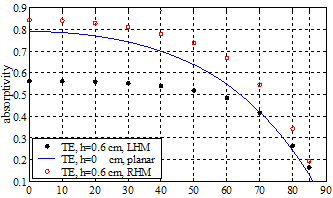
（a）TE波
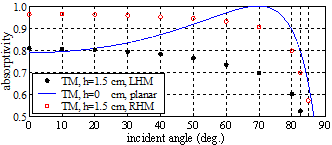
（b）TM波
图5 左手介质和右手介质指数相关随机粗糙面的电磁吸收率随入射角的变化曲线对比。f=10.5 GHz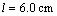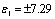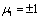，。，。均方根高度h=0表示是光滑平面，这时左手、右手介质的吸收是一样的，并在70°附近显示布儒斯特角效应
P. Xu and J. C. Shi, “Roughness effects on absorption and scattering of left-handed materials,” Radio Science, vol. 49, no. 6, pp. 400-414, 2014.
超材料（左手介质）周期性糙面也具备完全不同于正常介质（右手介质）的电磁吸收特性。如下图所示，超材料产生很大的±45°极化吸收差，和左右旋极化吸收差，正常介质则不能达到该效果。本研究不仅发现该现象，还从物理机理上进行了解释。未来可应用于超材料介电特性的新测量方法等。该研究成果成稿后拟投IEEE AP Trans.。
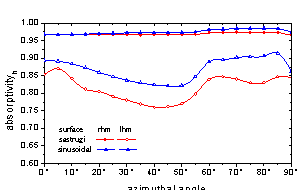
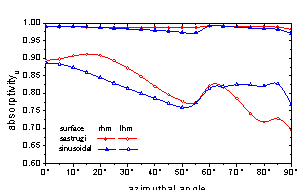
（a）水平极化 （b）垂直极化
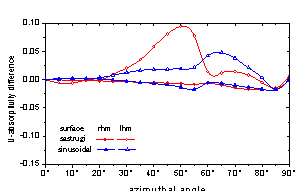
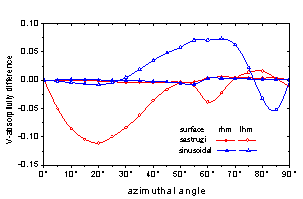
（c）±45°极化差 （d）左右旋极化差
图6 超材料与正常介质周期性粗糙面电磁吸收率对比
四、用于通信的电波传输
收发同向指收发均为右旋圆极化波（RR），收发反向指收为左旋圆极化、发为右旋圆极化（LR）。传输特性应用于通信，研究沿山地1.8米高处手机接收信号的变化规律，而散射特性应用于遥感，研究山地对卫星的回波信号特征（本问题未知量超300万，利用快速算法较好解决计算复杂度和存储问题）。如下图所示，本研究表明，山地传输信号特征具有完全不同于散射信号的特点：双站散射中，收发反向信号远大于同向信号；而在传输信号中则相反，收发反向信号远小于于同向信号。对其物理机理也进行了深入研究与阐释。
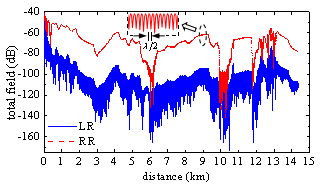
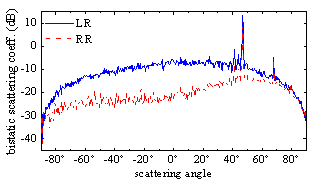
（a）山地圆极化电波传输特性 （b）山地圆极化电磁散射特性
图7 圆极化用于通信（传输特征）和遥感（散射特征）绝然相反
X. Chen, P. Xu*, X. Ma, Y. Yao, and H. Lv, “Abnormal circularly polarized propagation over terrain profile with Gaussian correlated roughness,” Progress In Electromagnetics Research Letters, vol. 104, pp. 169-177, 2022.
五、其它
1、FBAR滤波器TRL校准的仿真与测试
夹具嵌入的寄生效应影响薄膜体声波谐振腔（FBAR）滤波器的测试结果。针对目前发展状况和问题，提出一种改进的TRL校准测试方案，将三维电磁仿真和TRL计算相结合，用于测试套件（夹具和TRL校准件）的前期设计与优化，并且可以模拟实测情况，确保校准件的设计达标。实测中，由于滤波器真实参数未知，单组数据说服力不够，于是采用多种不同结构的测试套件测试同一个器件，多组测试结果高度吻合（见下图），且在通带内，各组结果之间的差异小于0.2 dB，不但精准确定了器件真实参数，而且表明TRL校准方法对于不同结构的夹具均能完成去嵌入。
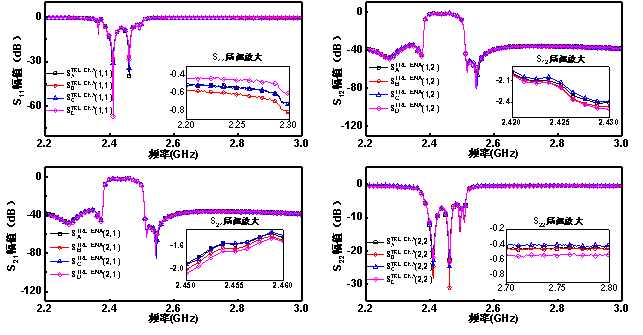
图8 TRL校准后S参数
丁文波，徐鹏，李劲等. FBAR滤波器TRL校准的仿真与测试，已投稿于中国测试，2022.
2、高斯坐标和瑞利坐标的应用
测量数据、模拟数据需与已知的统计分布曲线比对，以判断数据是否满足该分布。然而，仅仅依赖非线性曲线间的相似性，其判断往往不可靠，甚至错误，本文提出高斯坐标和瑞利坐标产生方法，从而分别将高斯和瑞利累积分布函数曲线都变换成直线，通过数据点是否在该直线上或均匀地分布在该直线两侧附近，直观而准确判断数据是否满足相应统计分布。该方法灵敏度极高且通用，且克服拟合优度的一定缺陷，可推广到其它非线性物理规律的判定。
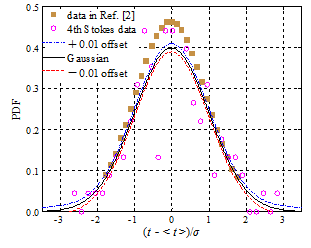
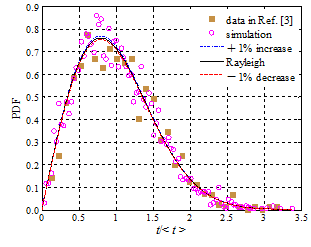
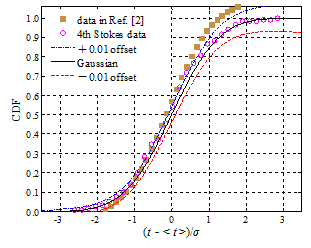
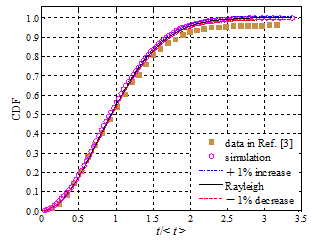
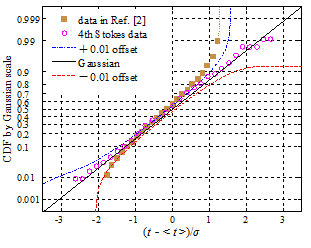
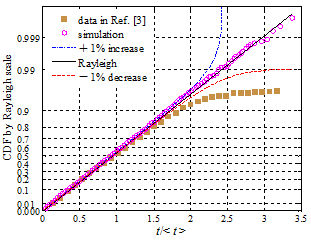
（a）高斯分布 （b）瑞利分布
图9 各自第3张图分别将高斯分布和瑞利分布曲线转换为直线，待评估数据是否为相关统计分布一目了然。传统方式是比对各自第1张图来判定是否满足相关分布，其有效性显著欠佳。
徐鹏，吕辉，黄楚云，“高斯坐标和瑞利坐标在电磁统计中的应用”，武汉大学学报（理学版）, vol. 68, no. 5, pp. 562-566, 2022.
